Typed version of some of my notes on NP and NP-Complete reductions for the Graduate Algorithms course I am taking. Attached at the bottom are various resources that I found helpful, so if you’ve stumbled upon this page somehow I recommend checking those out as well.
NP Reduction Steps
To show that a new problem of unknown difficulty is NP-Complete we have to do two main things.
- Show that the problem lies in NP.
- Show that the problem is NP-Hard.
If the problem both lies in NP and is shown to be NP-Hard then we can consider it NP-Complete! 😌
Show that the problem lies in NP
Showing that a problem lies in NP isn’t too difficult. To do this we need to think back to our definition of NP. A problem lies in NP if you can verify a solution to the problem (YES or NO) in polynomial time and you can solve the problem in nondeterministic polynomial time.
So what does this mean? Given a solution to the problem we need to show how we would verify it in polynomial time. Basically jot down the algorithm and do a quick runtime complexity analysis of it.
For example, to verify the Independent Set problem where we are given a graph G, a candidate solution set S, and a target minimum set size t we would do the following:
- Check each pair of vertices in S and verify there is no edge between them. For n vertices in S this would take O(n2) time.
- Verify the size of S is ≥ t. This would take O(n) time.
As you can see, we can verify the Independent Set problem in polynomial time so it lies in the class NP.
Show that the problem is NP-Hard
We can show that our new problem is NP-Hard by reducing another known NP-Hard problem to it in polynomial time. If we can do this, it shows that our new problem is at least as hard as the known problem. Let’s refer to the known NP-Hard problem as B and our new problem as A. Here are the high-level steps for reducing B to A.
Step 1 - Transform Input
Show that you can transform an input for B into an input for A in polynomial time. For 3-SAT -> k-Independent Set (k is our target t and equal to the number of clauses in the 3-SAT input) this would look like converting a CNF Formula into a graph where the variables in the formula (and their negations) are vertices.
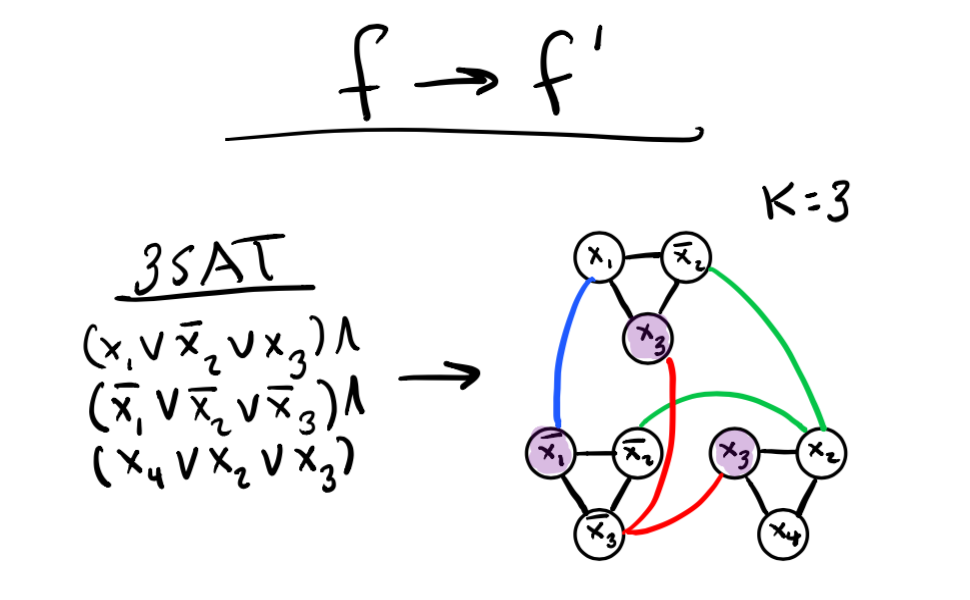
In the example above we create a triangle of vertices for each clause. We will choose to rely on satisfying a particular variable per clause by choosing it for our independent sets. To avoid accidentally relying on both a variable and its negation we connect these vertices with an edge. Since the definition of an independent set says that two vertices in the set cannot be connected by an edge, this inter-variable edge prevents us from choosing a contradicting set of assignments.
Step 2 - Use Blackbox for Problem A
Pretend you have a working polynomial time algorithm that can solve your new problem A and use it as a blackbox. Pass this algorithm your transformed input.
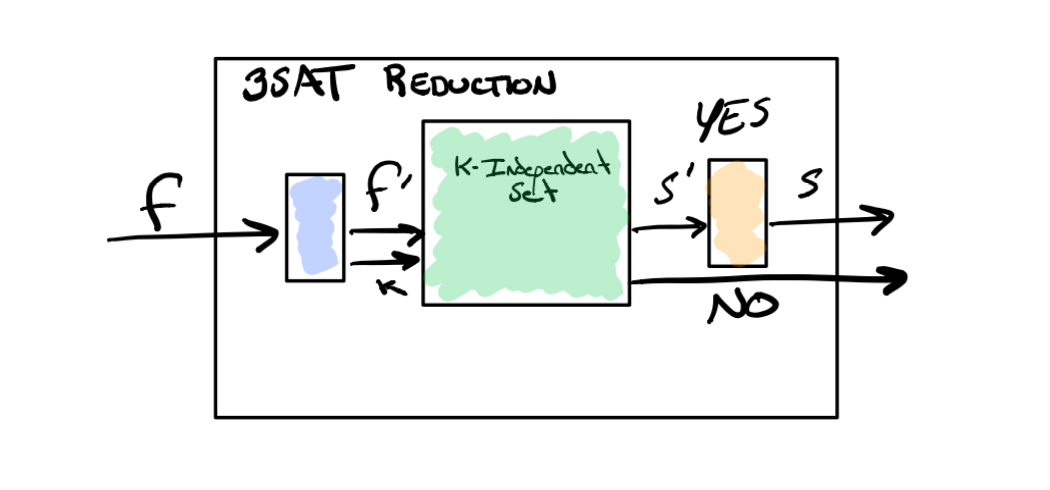
Step 3 - Transform Solution
Convert a solution to A into a solution for B. For the 3-SAT to Independent Set reduction this would mean using the set of independent vertices to create true/false variable assignments. Show why NO results for A also hold true for problem B.
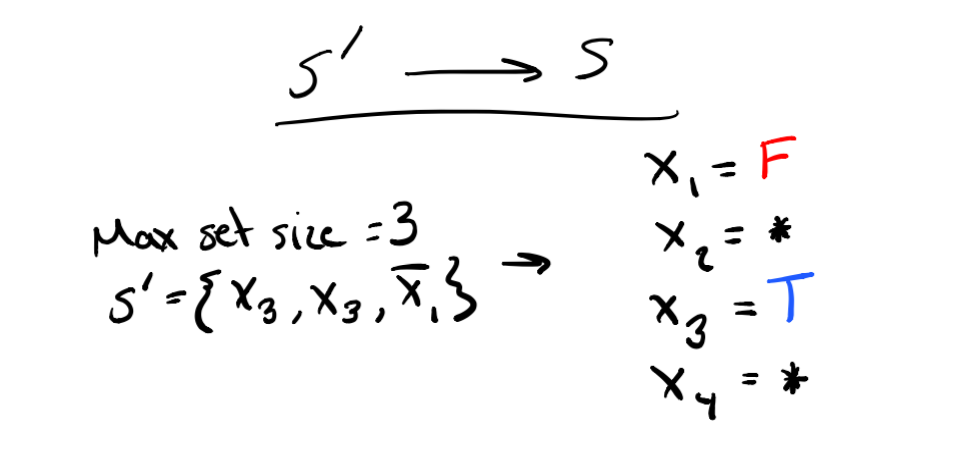
In the example above, the vertices in our independent set correspond with the variables X3 and not-X1 which means those must be satisfied. Since we’re not relying on X2 and X4 for anything they can be set to true or false, hence the wildcard.
Step 4 - Provide Proof
- Prove that if an arbitrary instance is YES for B, that it is also YES for A
- Prove that if a reduced instance is YES for A, that is is also YES for B
For this last proof you need to show that all instances that are produced from our reduction algorithm are valid in both – not arbitrary instances for A. By this I mean, the graphs we produce during the reduction are of a very particular structure. The Independent Set problem works on abritrary graphs of any structure and these don’t necessarily go A -> B.