Typed version of some of my notes on Linear Programming for the Graduate Algorithms course I am taking. Not formatted the best, but it gets the job done.

Linear programming provides a way of describing and solving optimization problems via the use of linear functions.

Standard Form of Primal LP

• max c^Tx
• subject to Ax ≤ b
• and x ≥ 0

Standard Form of Dual LP

• min b^Ty
• subject to A^Ty ≥ c
• and y ≥ 0

Example Primal LP

• max x₁ - 2x₃
• x₁ - x₂ ≤ 1
• 2x₂ - x₃ ≤ 1
• x₁,x₂,x₃ ≥ 0

Linear Algebra (Matrix) View of LP

We can view the Primal LP above as a series of matrices where b is a vector containing the coefficients of the objective function, A is a matrix containing the coefficients for each x variable in each of the constraints (the omission of a variable in a constraint results in a 0), and c is a vector containing the right-hand side value of each constraint inequality.

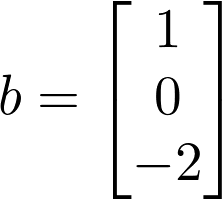
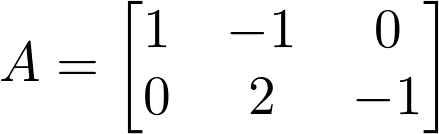
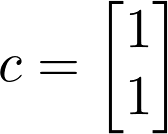
Finding Dual LP from Primal LP

My method for writing out the Dual LP:

Create a new variable y for each condition (except for the ≥ 0 constraints)

The objective function for the Dual LP will consist of the right side of the inequalities of the Primal LP as the coefficients for each y. For example the Primal LP above has the following constraints:

• x₁ - x₂ ≤ 1
• 2x₂ - x₃ ≤ 1

This would result in the following objective function for the Dual LP:

• min 1y₁ + 1y₂

Now we come up with the constraints for the Dual LP based on variables in the Primal LP. First let’s do the left-hand side of the inequalities:

• x₁ - x₂ ≤ 1

Becomes

• 1x₁y₁ - 1x₂y₁

and

• 2x₂ - x₃ ≤ 1

Becomes

• 2x₂y₂ - 1x₃y₂

Put these both together and we get:

• 1x₁y₁ - 1x₂y₁ + 2x₂y₂ - 1x₃y₂ ≥ 1y₁ + 1y₂

Now let’s factor out the x variables to create our constraints for our Dual LP.

• x₁(1y₁) + x₂(-1y₁ + 2y₂) + x₃(-1y₂)

We have three x variables so we’ll have three constraints. We’ll use the coefficiences of the x variables from the objective function of the Primal LP to use on the right-hand side of our Dual LP’s inequalities.

• x₁(1y₁)

Will give us this inequality:

• 1y₁ ≥ 1

And

• x₂(-1y₁ + 2y₂)

Will give us this inequality:

• -1y₁ + 2y₂ ≥ 0 (zero because x₂ is not in the objective function)

And

• x₃(-1y₂)

Will give us this inequality:

• -1y₂ ≥ -2

All in all this gives us the following Dual LP:

Example Dual LP

• min 1y₁ + 1y₂
• 1y₁ ≥ 1
• -1y₁ + 2y₂ ≥ 0
• -1y₂ ≥ -2
• y₁,y₂ ≥ 0

Converting LP into Standard (Canonical) Form

As you can see, the Dual LP above looks a bit different. It is minimizing instead of maximizing and using greater-than-or-equal-to instead of less-than-or-equal-to in its inequalities. We can convert it into standard for pretty simply, though.

Just multiply the objective function and both sides of the inequality by -1!

• max -1y₁ + -1y₂
• -1y₁ ≤ -1
• 1y₁ + -2y₂ ≤ 0
• 1y₂ ≤ 2
• y₁,y₂ ≥ 0

Determining if an LP is Infeasible

The feasible region of a linear program is the section of space where a valid point can lie. An LP is said to be infeasible when this feasible region is empty and therefore there is no valid assignment of its variables that can satisfy all of the LP’s constraints.

For example, take the following LP:

• max x₁ + x₂
• -1x₁ + -1x₂ ≤ -5
• 1x₁ ≤ 1
• 1x₂ ≤ 1
• x₁,x₂ ≥ 0

As you can probably tell, there is no way that we can have both x₁ and x₂ be both less than 1 and have their negated sum be less than 5. This LP is obviously infeasible. How can we programmatically determine this, though?

One was is by adding a new variable, z, to one of the constraints of our LP to create a new LP.

• -1x₁ + -1x₂ + z ≤ -5

z can be anything we need it to be. It can be as low as necessary to make this constraint feasible. What we want to see, though, is if we can find value of z such that z ≥ 0. If we can find one, this shows that z is not contributing anything to satisfy the inequality and that the original inequality without it is satisfiable on its own. We can determine this by creating a new objective function to maximize z.

• max z
• -1x₁ + -1x₂ + z ≤ -5
• 1x₁ ≤ 1
• 1x₂ ≤ 1
• x₁,x₂ ≥ 0

Like I said earlier, if z ≥ 0 then the original LP is feasible. If not, then the LP is infeasible. For the other constraints we could add additional variables to do the same (e.g. z₁, z₂, …)

Determining if an LP is Unbounded

A linear program is said to be unbounded if its objective function can be made arbitrarily large for maximization or small for minimization. How can we tell if an LP is unbounded?

We can use the Dual LP!

The Dual LP gives us an upper bound on the objective function of the Primal LP.

• c^Tx ≤ b^Ty

This is known as the weak duality theorem. Some facts from the theorem:

• If the Primal LP is unbounded, the Dual LP is infeasible
• If the Dual LP is unbounded, the Primal LP is infeasible
• If the Dual LP is infeasible, the Primal LP is either unbounded or infeasible

We can use these facts to determine if our Primal LP is unbounded or not.

1. First check and see if the Primal LP is infeasible using the z variable approach described above.
2. If it is feasible then find the Dual LP and check to see if it is feasible or not using the z variable technique.
3. If the Dual LP is infeasible and we found our Primal LP to be feasible then we know the Primal LP must be unbounded. If the Dual LP is feasible then our Primal LP is bounded.

Strong Duality Theorem

Primal LP is feasible and bounded iff Dual LP is feasible and bounded

If there is an optimal point for the Primal then there is an optimal point for the Dual.