In one of our labs in Georgia Tech’s Intro to High Performance Computing course, we had to explore the parallel computing problem of list ranking. This lecture by Professor Vuduc does a better job explaining than I can, but list ranking is essentially just traversing a linked list and assigning each node a “rank”, or distance from the list’s head. A serial implementation of list ranking is trivial and can be completed in O(n) time by walking the list. A parallel implementation is a bit trickier. In our lab we researched and implemented two such algorithms: Wyllie’s and Helman/JáJá’s. I found Wyllie’s algorithm to be easy enough to grok, but Helman and JáJá’s was a different story. It felt like there was a dearth of simple explanations for the algorithm outside of academic papers so this post is my attempt at rectifying that.

Array Pool Representation of Linked Lists

To operate on and access a linked list in parallel we need to rethink our representation of it. It can’t simply be a loose collection of node that contain pointers to each other since there is no way of discovering/accessing the nodes out of order that way. Instead, we need to represent the linked list using an array. Professor Vuduc refers to this as an array pool representation. I found this naming confusing at first since it made me think of an object pool consisting of a bunch of arrays. It’s not that, though. It’s a pool of list nodes that just happens to be represented by an array. Regardless of the naming, using an array pool let’s us represent a linked list using a single contiguous piece of memory. Consider the arrays below:

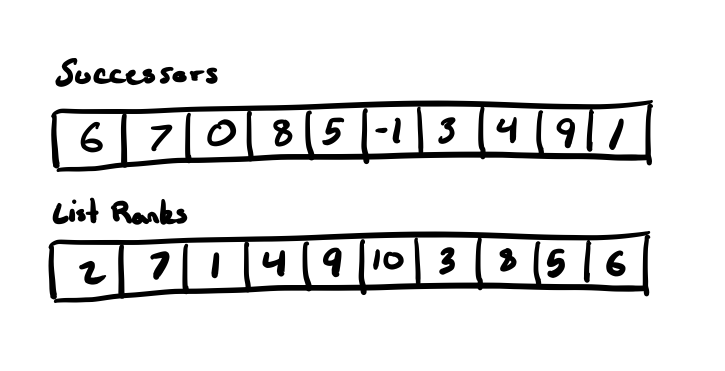
The Successors array represents the “next” pointers for each node in a linked list and each “next” pointer corresponds with an index in the array. The List Ranks array represents the “value” for each node in the linked list at a given index. Or in other words, Successors[0] and List Ranks[0] both refer to the same logical linked list node, they just contain different attributes of the node.

To make it easier to visualize, in the example above each node has its list rank as its value. In practice, however, a node’s value could be anything. For the algorithm descriptions that follow we will assume our implementation is using an array pool to represent the list.

Glossary

I will be using the following variables throughout:

• P - Number of processors
• n - Number of nodes in the list
• s - Number of sublists

Wyllie’s List Ranking Algorithm

Wyllie’s algorithm takes a divide-and-conquer approach by continuously splitting the list into smaller sublists via a technique known as pointer jumping. This lecture does a good job of explaining the algorithm and there are lots of resources online so I won’t go into too much detail. In terms of work and span analysis, Wyllie’s algorithm has a span of O(log²n) and work of O(nlogn). As you can see, it has to do significantly more work than the serial algorithm so you need to have a large value of n and a high amount of available processors to make Wyllie’s approach worthwhile. This is where Helman and JáJá’s algorithm comes in.

Helman and JáJá’s List Ranking Algorithm

Helman and JáJá describe their approach to the list ranking problem with a span of O(n/P) and work of O(n) in their paper Designing Practical Efficient Algorithms for Symmetric Multiprocessors (for more information on the performance analysis of the algorithm I recommend checking out this paper). I found their paper pretty dense, however, and realized that there was a lack of approachable explanations for it online. Here’s my attempt at explaining it step-by-step.

Split the List into Sublists

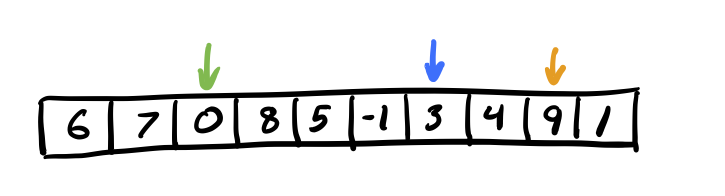
Split the linked list into sublists by randomly choosing at least P - 1 sublist heads in addition to the list’s true head to create s sublists. This in theory will allow us to divide up sequential list-ranking of each sublist across the P processors. However, since we’re randomly choosing sublist heads there is the potential for the work to be distributed unevenly. So, in practice, I actually saw improved performance by choosing a value of s that was greater than P and allowing OpenMP to sort of load balance the work across the processors. In the diagram below we’re randomly selecting 2 sublist heads (indices 6 and 8) in addition to the list’s true head (index 2):

Traverse Each Sublist in Parallel and Compute Partial List Rankings

Now, in parallel, we can traverse each sublist – stopping when we reach the head of another sublist. In the diagram below, consider the green, blue, and orange traversals to be occurring on distinct processors.

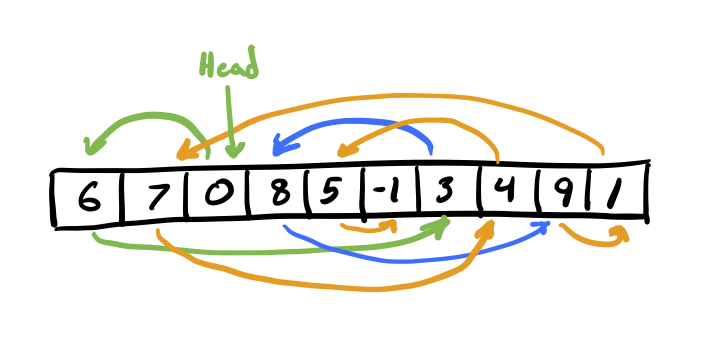
While walking these sublists, we sequentially compute the list ranking for the sublist on each processor. After we’re done, we should have these partial rankings in our List Ranking array. Whenever we reach the end of a sublist we record the total rank of our current sublist and the index of the next sublist’s head for use in the next step. See the diagram below for what the current state of our List Ranking array will look like:

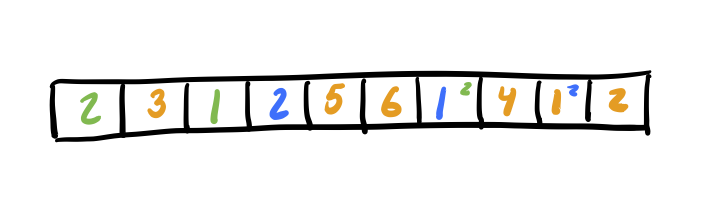
Sequentially Compute the List Rankings of the Sublist Heads

As mentioned earlier, we should have recorded the total rank for each sublist along with the index of the head of the following sublist. We can use that data to sequentially compute the starting rank offsets for each sublist.

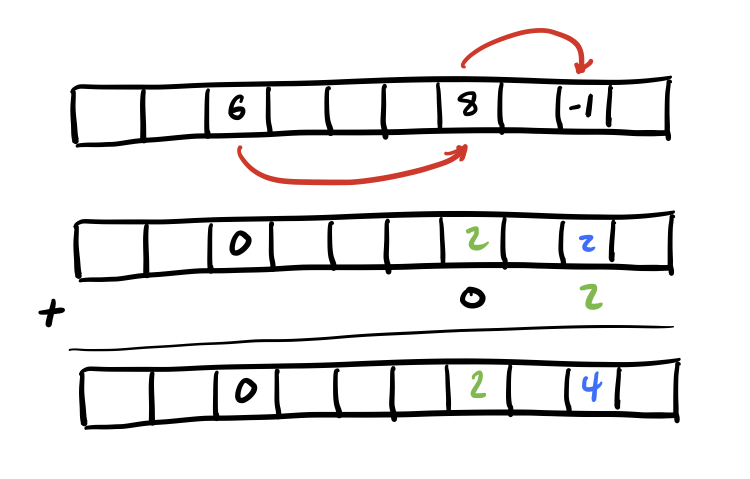
As you can see in the diagram above, we can walk across the sublist heads themselves in the correct order since we recorded each sublist’s successor index. Since we recorded the total rank as well for each sublist we can just accumulate these values using a prefix sum operation.

Apply the Sublist Head Rank Offsets in Parallel

Now, in parallel, we can apply the rank offsets we computed for each sublist head to all of the nodes in each sublist. The diagram below demonstrates what this might look like:

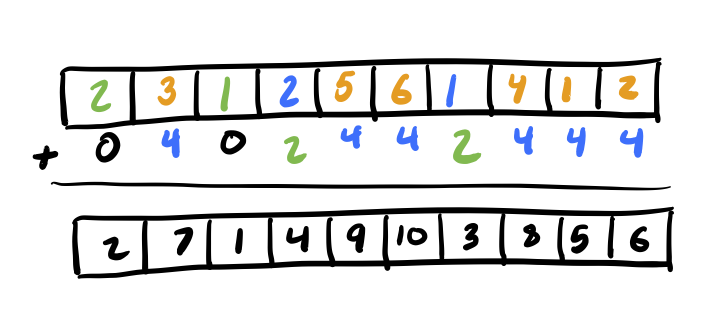
If you’ve done some basic bookkeeping to track which sublist a node belongs to, this can be done as a massively parallel operation using a simple parallel for loop across all of the elements at once. As you can see in the diagram above, this results in the List Ranks array containing the final list ranking values for the linked list.

Other Resources

Hopefully you found this explanation helpful. If you’re still stumped, the following resources helped me during implementation.

1. Designing Practical Efficient Algorithms for Symmetric Multiprocessors (excerpt from original Helman and Jájá paper)
2. A Comparison of the Performance of List Ranking and Connected Components Algorithms on SMP and MTA Shared-Memory Systems
3. List Ranking on Multicore Systems

If you have any suggestions or feedback for this post feel free to create an issue. And always remember, dream big!